From the equivalent circuit it is evident that the current produced by the solar cell is equal to that produced by the current source, minus that which flows through the diode, minus that which flows through the shunt resistor:
- I = IL − ID − ISH
where
- I = output current (amperes)
- IL = photogenerated current (amperes)
- ID = diode current (amperes)
- ISH = shunt current (amperes).
The current through these elements is governed by the voltage across them:
- Vj = V + IRS
where
- Vj = voltage across both diode and resistor RSH (volts)
- V = voltage across the output terminals (volts)
- I = output current (amperes)
- RS = series resistance (Ω).
By the Shockley diode equation, the current diverted through the diode is:
where
- I0 = reverse saturation current (amperes)
- n = diode ideality factor (1 for an ideal diode)
- q = elementary charge
- k = Boltzmann's constant
- T = absolute temperature
- At 25°C,
 volts.
volts.
By Ohm's law, the current diverted through the shunt resistor is:
where
- RSH = shunt resistance (Ω).
Substituting these into the first equation produces the characteristic equation of a solar cell, which relates solar cell parameters to the output current and voltage:
An alternative derivation produces an equation similar in appearance, but with V on the left-hand side. The two alternatives are identities; that is, they yield precisely the same results.
In principle, given a particular operating voltage V the equation may be solved to determine the operating current I at that voltage. However, because the equation involves I on both sides in a transcendental function the equation has no general analytical solution. However, even without a solution it is physically instructive. Furthermore, it is easily solved using numerical methods. (A general analytical solution to the equation is possible using Lambert's W function, but since Lambert's W generally itself must be solved numerically this is a technicality.)
Since the parameters I0, n, RS, and RSH cannot be measured directly, the most common application of the characteristic equation is nonlinear regression to extract the values of these parameters on the basis of their combined effect on solar cell behavior.
Open-circuit voltage and short-circuit current
When the cell is operated at open circuit, I = 0 and the voltage across the output terminals is defined as the open-circuit voltage. Assuming the shunt resistance is high enough to neglect the final term of the characteristic equation, the open-circuit voltage VOC is:
Similarly, when the cell is operated at short circuit, V = 0 and the current I through the terminals is defined as the short-circuit current. It can be shown that for a high-quality solar cell (low RSI0, and high RSH) the short-circuit current ISC is: and

![I_{D} = I_{0}
\left\{\exp\left[\frac{qV_{j}}{nkT}\right] - 1\right\}](http://upload.wikimedia.org/math/b/8/d/b8d0ebea3f33be0c023cf7b8a30cb717.png)
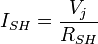
![I = I_{L} - I_{0} \left\{\exp\left[\frac{q(V +
I R_{S})}{nkT}\right] - 1\right\} - \frac{V + I R_{S}}{R_{SH}}.](http://upload.wikimedia.org/math/4/7/d/47d17d3c2fe8840d0b3181860bd22f0a.png)


No comments:
Post a Comment